Gamma-Gamma-Verteilung

Die Gamma-Gamma-Verteilung ist eine univariate Verteilung für stetige Zufallsvariablen, die in der Bayesschen Statistik und in der Inferenztheorie eine wichtige Rolle spielt, da es sich um eine Mischverteilung handelt.

Definition

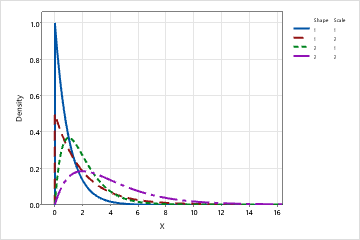
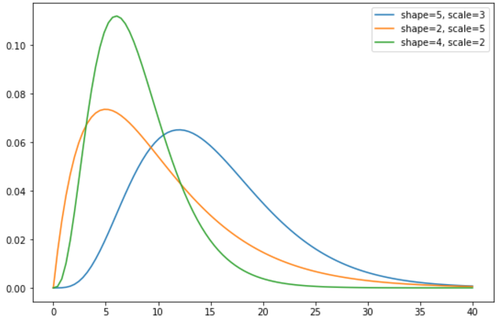
Die Wahrscheinlichkeitsdichtefunktion der Gamma-Gamma-Verteilung ${\displaystyle Gg(\alpha ,\beta ,\delta )}$ ist bei ${\displaystyle \alpha ,\beta ,\delta >0}$

${\displaystyle f(x)={\frac {\beta ^{\alpha }}{B(\alpha ,\delta )}}{\frac {x^{\delta -1}}{(\beta x)^{\alpha \delta }}}}$

wobei ${\displaystyle B(\alpha ,\beta )}$ die Eulersche Betafunktion ist.

Eigenschaften

Erwartungswert und Varianz

Der Erwartungswert ist

${\displaystyle \operatorname {E} (X)={\frac {\delta \beta }{\alpha -1}}}$, für ${\displaystyle \alpha >1}$

und die Varianz

${\displaystyle \operatorname {Var} (X)={\frac {\beta ^{2}\delta (\delta \alpha -1)}{(\alpha -1)^{2}(\alpha -2)}}=\operatorname {E} (X)^{2}{\frac {1 {\frac {\alpha -1}{\delta }}}{\alpha -2}}}$, für ${\displaystyle \alpha >2}$

Modus

Der Modus ist

${\displaystyle \operatorname {Mod} (X)={\frac {\beta \ (\delta -1)}{\alpha 1}}}$, für ${\displaystyle \delta >1}$

Sonderfall δ=1

Falls δ=1, dann ist die Dichtefunktion

${\displaystyle f(x|\delta =1)={\frac {\alpha }{\beta x}}\left({\frac {\beta }{\beta x}}\right)^{\alpha }}$

Da ${\displaystyle G(1,\lambda )=Exp(\lambda )}$ wendet man diesen Sonderfall an der Exponentialverteilung, mit gammaverteiltem ${\displaystyle G(\alpha ,\beta )}$ Parameter ${\displaystyle \lambda }$.

Sonderfall β=1: Inverse Betaverteilung

Eine Gamma-Gamma-Verteilung ${\displaystyle Gg(\alpha ,\beta =1,\delta )}$ entspricht einer inversen Betaverteilung ${\displaystyle {\mathcal {InvB}}(a=\delta ,b=\alpha )}$

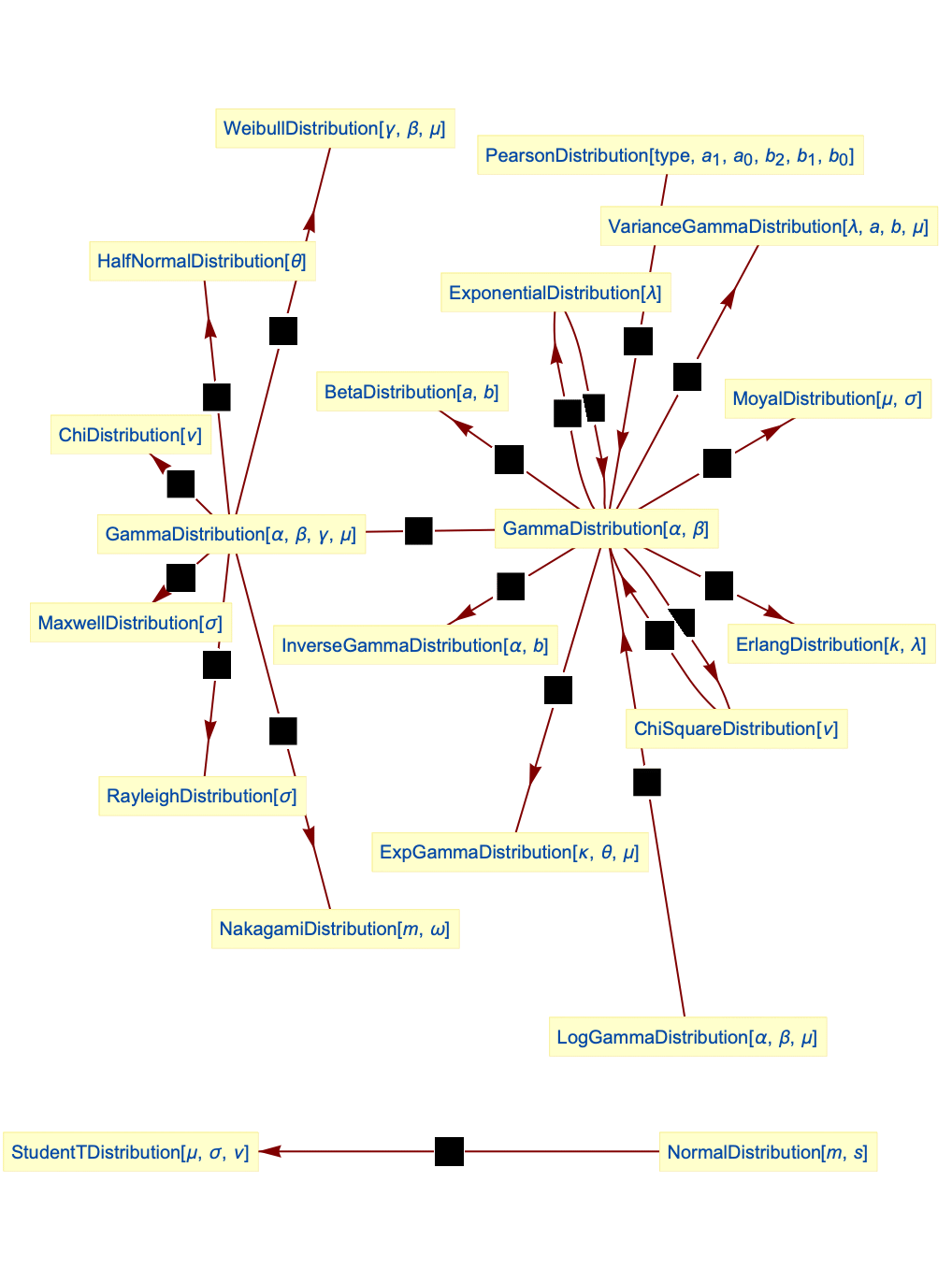
Beziehung zur Gammaverteilung

Ist der zweite Parameter ${\displaystyle \epsilon }$ der Gammaverteilung ${\displaystyle G(d,\epsilon )}$ eine Zufallsvariable, die wie eine Gammaverteilung ${\displaystyle G(a,b)}$ verteilt ist, dann ist die hervorgehende Zufallsvariable wie eine Gamma-Gamma-Verteilung ${\displaystyle G(a,b,d)}$ verteilt.

Beziehung zur Exponentialverteilung

Ist der Parameter ${\displaystyle \lambda }$ der Exponentialverteilung ${\displaystyle Exp(\lambda )}$ eine Zufallsvariable, die wie eine Gammaverteilung ${\displaystyle G(a,b)}$ verteilt ist, dann ist die hervorgehende Zufallsvariable wie eine Gamma-Gamma-Verteilung ${\displaystyle G(a,b,1)}$ verteilt.

Literatur

• Leonhard Held: Methoden der statistischen Inferenz. Likelihood und Bayes, unter Mitwirkung von Daniel Sabanés Bové, Spektrum Akademischer Verlag, Heidelberg 2008, ISBN 978-3-8274-1939-2

Siehe auch

• Exponentialverteilung